BÀI 1 + 2
PHÉP BIẾN HÌNH – PHÉP TỊNH TIẾN
–o0o–
1. Định nghĩa : PHÉP BIẾN HÌNH
Quy tắc tương ứng mỗi điểm M của mặt phẳng với một điểm duy nhất M’ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.
Kí hiệu :
F(M) = M’
Nếu H là hình nào đó trong mặt phẳng thì
ta kí hiệu : H’ = F(H) là tập hợp các điểm M’ = F(M) với mọi M thuộc H.
khi đó, ta nói F là phép biến hình H thành hình H’.
Trong đó : M’ là ảnh của M qua phép biến hình FVí dụ :
- M’ là điểm đối xứng của M qua I. ta gọi M’ là ảnh của M qua phép biến hình F đối xứng tâm I.
- Đường kính AB của đường tròn (O) là trục đối xứng. lấy dây M’M vuông góc AB tại H. ta gọi M’ là ảnh của M qua phép biến hình F đối xứng trục AB…
Định nghĩa :
Trong mặt phẳng cho vectơ 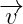 . phép biến hình biến mỗi điểm M thành M’ sao cho :
. phép biến hình biến mỗi điểm M thành M’ sao cho :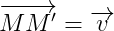 được gọi là phép tịnh tiến theo vectơ
được gọi là phép tịnh tiến theo vectơ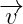 .
.
Kí hiệu :
T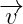 (M) = M’ <=>
(M) = M’ <=> 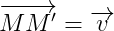
Tính chất :Định lí 1 :
Nếu phép tịnh tiến biến hai điểm M và N lần lượt thành M’ và N’ thì MN =M’N’.
T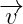 (M) = M’ và T
(M) = M’ và T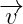 (N) = N’ => MN =M’N’.
(N) = N’ => MN =M’N’.
Định lí 2 :
Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó.
Hệ quả :
Phép tịnh tiến biến đường thẳng thành
đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng, biến
tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có
cùng bán kính, biến góc thành góc bằng nó.
Biểu thức tọa độ của Phép tịnh tiến :
Trong mặt phẳng tọa độ Oxy, cho Phép tịnh tiến theo vectơ 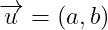 .
.
Ta có M(x, y) và M’(x’, y’), T (M) = M’ ta có :
(M) = M’ ta có :
====================
BÀI TẬP SGK :
BÀI 2 TRANG 7 SGK CB :Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ
Giải.
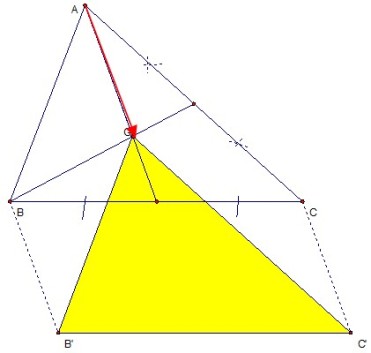 Xác định ảnh của tam giác ABC :
Xác định ảnh của tam giác ABC :T
Hay A’ trùng G.
T
T
Vậy : T
T
Hay A là trung điểm của DG.
BÀI 3 TRANG 7 SGK CB :
Trong mặt phẳng Oxy cho vectơ
a) Tìm tọa độ A’, B’ lần lược là ảnh của A, B qua phép tịnh tiến theo vectơ
b) Tìm tọa độ C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ
c) Tìm phương trình d’ là ảnh của d qua phép tịnh tiến theo vectơ $latex.
Giải.
a) TVậy A’(2; 7).
Tương tự tìm B’
b)
T (C) = A ta có :
(C) = A ta có :
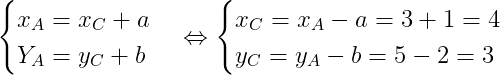
Vậy C(4;3)
c)T
Vậy C(4;3)
T (d) = d’
(d) = d’
Lấy M(x; y) thuộc d.
T (M) = M’thuộc d’ ta có :
(M) = M’thuộc d’ ta có :
Thế vào d ta được :
(x’ + 1) – 2(y’ – 2) + 3 = 0
<=> x’ -2y’ + 8 = 0
Vậy : d’ có phương trình : x – 2y +8 = 0
Bài toán 1 SKG NC trang 7 :Cho hai điểm B, C cố định trên đường tròn (O, R) và điểm A thay đổi trên đường tròn đó. Chứng minh rằng trực tân H của tam giác ABC nằn trên đường tròn cố định.
Giải.
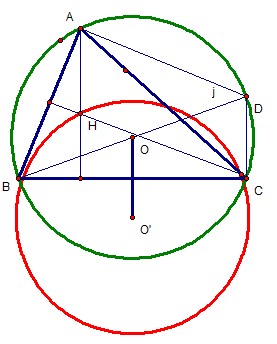 Kẽ đường kính BD.
Kẽ đường kính BD.Xét tứ giác AHCD ta có :
AH // DC (cùng vuông góc BC)
CH // DA (cùng vuông góc BA)
=> tứ giác AHCD hình bình hành.
=>
=> H = T
MÀ : A thay đổi trên đường tròn (O; R) nên H nằm trên đường tròn (O’, R) là ảnh của đường tròn (O; R) qua phép tịnh tiến
========================
BÀI TẬP RÈN LUYỆN :
BÀI 1 : Cho đường tròn (O) và hai điểm A, B. một điểm M chạy trên đường tròn (O). tìm quỹ tích của điểm M’ sao cho :Bài 2 :cho tam giác ABC vuông tại A. từ điểm P thay đổi trên BC vẽ PE vuông góc AB, PF vuông góc AC. Tìm tập hợp điểm M sao cho ME/MF = 1/3.
$\frac{1}{2}$
Trả lờiXóaNhận xét này đã bị tác giả xóa.
Trả lờiXóa[cc lang="latex"]$$\frac{3}{\sin x}$$[/cc]
Trả lờiXóa