BÀI 2 Phương trình quy về phương trình bậc nhất và phương trình bậc hai

BÀI 2

Phương trình quy về phương trình bậc nhất và phương trình bậc hai

–o0o–

1. Phương trình bậc nhất :

Định nghĩa : 

phương trình bậc nhất có dạng : ax + b = 0 (1)

cách giải :
(1) ⇔ ax = – b

Nếu a ≠ 0 thì x =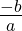

 Nếu a = 0 thì 0.x = – b

Nếu b = 0  thì phương trình (1) vô số nghiệm.

Nếu b ≠ 0  thì phương trình (1) vô nghiệm.

2. Phương trình bậc hai :

Định nghĩa :

phương trình bậc hai có dạng : ax² + bx + c = 0 (a ≠ 0)

Cách giải :
Tính biệt số : 𝛥 = b² – 4ac

Nếu 𝛥 < 0 thì phương trình (2) vô nghiệm.

Nếu 𝛥 = 0 thì phương trình (2) có nghiệm kép :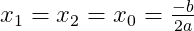

 Nếu 𝛥 > 0 thì phương trình (2) có 2 nghiệm phân biệt :

Định lí viet  thuận :

Nếu phương trình bậc hai có dạng : ax² + bx + c = 0 (a ≠ 0) có 2 nghiệm phân biệt x₁, x₂ thì

• 
• 

Định lí viet  đảo :
Nếu ta có hai số u, v có u + v = S và u.v = P thì u và v là nghiệm của phương trình :

X² – SX + P = 0

CÁC DẠNG TOÁN :

PHƯƠNG TRÌNH CHỨA ẨN TRONG DẤU GIÁ TRỊ TUYỆT ĐỐI :
CÁCH GIẢI :
      C1 : Định nghĩa :

C2 : Bình phương hai vế phương trình không âm.
C3 : Công thức :

• |A| = |B| ⇔ A = ± B
• |A| = B ⇔
• |A| + |B| = 0 ⇔ A =  B = 0

Bảng xét dấu (chương sau sẽ học).

PHƯƠNG TRÌNH CHỨA ẨN TRONG DẤU CĂN :

C1 :Bình phương hai vế phương trình không âm.
 C2 :Công thức :

• ⇔
• ⇔

=====================

BÀI TẬP SGK CB :

BÀI 6 TRANG 62 :
a)| 3x – 2| = 2x + 3 (a)

giải.

C1 : Định nghĩa :

Nếu 3x – 2 ≥ 0 ⇔ x ≥ 2/3 thì

(a) trở thành : 3x – 2 = 2x +3 ⇔ x = 5≥ 2/3  (nhận).

Nếu 3x – 2 < 0 ⇔ x < 2/3 thì

(a) trở thành : -3x + 2 = 2x +3 ⇔ 5x = -1 ⇔ x = -1/5 < 2/3 (nhận).

Vậy : S = {-1/5; 5}.

C2 : Bình phương hai vế phương trình không âm.

Nếu 2x + 3 < 0 thì phương trình vô nghiệm (| 3x – 2| ≥ 0).

Nếu 2x + 3 ≥ 0 ⇔ x ≥ -3/2 thì :

(| 3x – 2|)² = (2x + 3)²

⇔ 5x² – 24x – 5  = 0

⇔ x = -1/5≥ -3/2  v x = 5

So với x ≥ -3/2 , vậy : S = {-1/5; 5}.

C3 : Công thức :

| 3x – 2| = 2x + 3

⇔

⇔  x = 5 v x = -1/5

vậy : S = {-1/5; 5}.

BÀI 7 TRANG 63 :
a)     
b)     
Giải.

⇔
⇔
⇔
⇔
⇔ x = 15
Vậy S = {15}.
——————————————-
b)
Đk :
> 0
⇔
⇔
⇔
⇔
⇔
⇔
⇔ x =-1
Vậy S = {-1}.

===========================================

BÀI TẬP BỔ SUNG :

BÀI 1 :
Giải và biện luận phương trình : mx + m² – 2m = 0 (*)

Giải

Ta có  : a = m ; b = m² – 2m = m(m – 2)
Nếu a  = m ≠ 0

thì (*) có một nghiệm : x =

 Nếu a = m = 0 thì 0.x = 0(2- 0) = 0

thì b = 0  thì phương trình (*) vô số nghiệm.

vậy :

• m ≠ 0 : (*) có một nghiệm : x = 2-m
• m = 0 : phương trình (*) vô số nghiệm.

—————————————————————————————-
BÀI 2 :
Cho phương trình : (m + 2)x + 3m – 5= 0 (1)

1. Định m để phương trình (1) có nghiệm x = 2.
2. Định m để phương trình (1) vô nghiệm.

Giải.

để phương trình (1) có nghiệm x = 2 khi :
(m + 2).2 + 3m – 5= 0
⇔ 5m – 1 = 01/5
⇔ m = 1/5
b. a = m + 2 ; b = 3m – 5.
Định m để phương trình (1) vô nghiệm khi :

vậy : m = 2.

BÀI 3 :

Cho đường thẳng d : y = (m – 1)x – 2m – 7. Chứng minh rằng : đường thẳng d luôn đi qua một điểm cố định.

Giải.

Nếu đường thẳng d luôn đi qua một điểm A(x,y) cố định thì

y = (m – 1)x + 2m – 7 luôn đúng mọi m.

(x – 2)m  – x – y – 7 = 0 luôn đúng mọi m khi :

Vậy : đường thẳng d luôn đi qua một điểm cố định A(2; -9).

===============================================

ĐỀ THI ĐẠI HỌC :

Khối B – 2011 :
2.Giải phương trình :

Khối A – 2009 :
2.Giải phương trình :
ĐÁP ÁN :

Khối A – 2007 :
Tìm m để phương trình có nghiện thực :
Đáp Án : -1 < m  ≤ 1/3.
Khối B – 2007 :
Chứng minh rằng với mọi giá trị dương của tham số m, phương trình sau có hai nghiệm thực phân biệt: x² + 2x – 8 =
Đáp Án : m > 0.
Khối D – 2005 :
2.Giải phương trình :