Gia sư toán - lý - hóa tp Hồ Chí Minh

Đào tạo + Gia sư TOÁN - Lý - HÓA tp Hồ Chí Minh

Thứ Sáu, 28 tháng 9, 2012

Bài 1 – 2 : Véctơ – tổng và hiệu hai véctơ

Bài 1 – 2

Véctơ – tổng và hiệu hai véctơ.

–o0o–

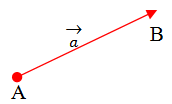
1. Khái niệm :
Véctơ là một đoạn thẳng có hướng.
  • Kí hiệu : \overrightarrow {AB}
Trong đó : AB : đoạn thẳng; A là điểm đầu; B là  điểm cuối.
  • Đặc điểm :
  1. Phương (giá) : đường thẳng AB.
  2. Chiều : từ A đến B.
  3. Độ lớn :  |\overrightarrow {a}| = |\overrightarrow {AB}| = AB
  • Ngoài ra : dung các kí tự thường : \overrightarrow {a} = \overrightarrow {AB}
  • Ý nghĩa : biểu diển lực, vận tốc, gia tốc…
2. Véctơ cùng phương, Véctơ cùng hướng.
Hai Véctơ gọi là Véctơ cùng phương khi giá của chúng trùng nhau hoặc song song.
Hai Véctơ gọi là Véctơ cùng hướng khi chúng cùng phương và cùng chiều.
Hai Véctơ gọi là Véctơ ngược hướng khi chúng cùng phương và ngược chiều.

Kí hiệu :
  • \overrightarrow {a} // \overrightarrow {b} : hai cùng phương.
  • \overrightarrow {a} \uparrow\uparrow \overrightarrow {b} : hai cùng hướng .
  • \overrightarrow {a} \uparrow\downarrow\overrightarrow {b} : hai ngược hướng.
3. Hai Véctơ bằng nhau :
Hai Véctơ gọi là bằng nhau  khi chúng cùng hướng và cùng độ lớn.
Kí hiệu : \overrightarrow {a} = \overrightarrow {b}
Lưu ý :

  • Véctơ có độ lớn bằng 1 gọi là véctơ đơn vị .
  • Véctơ có độ lớn bằng 0 gọi là véctơ không . Kí hiệu : \overrightarrow {0}
2.Tổng hai véctơ :
\overrightarrow {a} + \overrightarrow {b} = ?
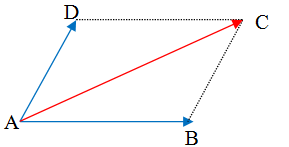hình bình hànhQuy tắc hình bình hành :
\overrightarrow {AB} + \overrightarrow {AD} =\overrightarrow {AC}
Ba điểm A, B, M tùy ý : \overrightarrow {AB}=\overrightarrow {AM}+ \overrightarrow {MB}
Tính chất :
  1. Tính giao hoán : \overrightarrow {a} + \overrightarrow {b} = \overrightarrow {b} + \overrightarrow {a} .
  2. Tính kết hợp : (\overrightarrow {a} + \overrightarrow {b})+\overrightarrow {c}= \overrightarrow {a} + (\overrightarrow {b}+\overrightarrow {c})
  3. Tính cộng vectơ không : \overrightarrow {a} + \overrightarrow {0} = \overrightarrow {0} + \overrightarrow {a}=\overrightarrow {a} .
Hiệu hai vectơ :
Vectơ đối của vectơ \overrightarrow {a} là một vectơ ngược hướng và cùng độ lớn vectơ \overrightarrow {a}.
Kí hiệu : vectơ -\overrightarrow {a}.
Ta có : : \overrightarrow {a} - \overrightarrow {b} = \overrightarrow {a} + (-\overrightarrow {b}).
Ba điểm A, B, M tùy ý : \overrightarrow {AB}=\overrightarrow {MB}- \overrightarrow {MA}.

====================================

BÀI TẬP SGK :

BÀI 3 TRANG 7 SGK CB :
Cho tứ giác ABCD, Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi \overrightarrow {AB} = \overrightarrow {DC}.

GIẢI.

Ta có, ABCD là hình bình hành :
=>AB // DC và AB = DC
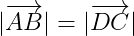
hay \overrightarrow {AB}, \overrightarrow {DC} cùng hướng và |\overrightarrow {AB}|= |\overrightarrow {DC}|
=> \overrightarrow {AB} = \overrightarrow {DC}
Ta lại có,  \overrightarrow {AB} = \overrightarrow {DC}  :
=>\overrightarrow {AB}, \overrightarrow {DC} cùng hướng và |\overrightarrow {AB}|= |\overrightarrow {DC}|
hay AB // DC và AB = DC
=>ABCD là hình bình hành
BÀI 4 TRANG 7 SGK CB :
Cho hình lục giác đều ABCDEF có tâm O.
  1. Tìm Véctơ khác \overrightarrow {0} và cùng phương \overrightarrow {OA}.
  2. Tìm Véctơ bằng \overrightarrow {AB}.

GIẢI.

1. Các Véctơ khác \overrightarrow {0} và cùng phương \overrightarrow {OA} :
\overrightarrow {OD};\overrightarrow {DO};\overrightarrow {DA};\overrightarrow {AD};\overrightarrow {BC}\overrightarrow {CB};\overrightarrow {EF}; \overrightarrow {FE}.
Véctơ bằng \overrightarrow {AB} :
\overrightarrow {ED}; \overrightarrow {OC}; \overrightarrow {FO}.
BÀI 3 TRANG 12 SGK CB :
Chứng minh rằng đối mọi tứ giác ABCD bất kỳ, ta luôn có :
  1. \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA}=\overrightarrow {0}
  2. \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CB} - \overrightarrow {CD}

GIẢI.

  1. Ta Áp dụng quy tắc 3 điểm cho phép cộng vectơ :
\overrightarrow {AB} + \overrightarrow {BC}= \overrightarrow {AC}
\overrightarrow {CD} + \overrightarrow {DA}= \overrightarrow {CA}
TA CÓ : \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA}= \overrightarrow {AC} + \overrightarrow {CA}=\overrightarrow {AA}= \overrightarrow {0}
2.Ta Áp dụng quy tắc 3 điểm cho phép trừ vectơ :
\overrightarrow {AB} - \overrightarrow {AD}= \overrightarrow {DB}
\overrightarrow {CB} - \overrightarrow {CD}= \overrightarrow {DB}
=> \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CB} - \overrightarrow {CD}
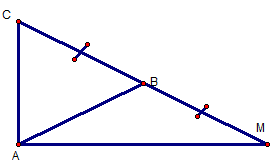
BÀI 5 TRANG 12 SGK CB :
Cho tam giác đều ABC cạnh a. tính độ dài các vectơ :
\overrightarrow {AB} + \overrightarrow {BC}
\overrightarrow {AB} - \overrightarrow {BC}

GIẢI.

Ta Áp dụng quy tắc 3 điểm cho phép cộng vectơ :
\overrightarrow {AB} + \overrightarrow {BC}=\overrightarrow {AC}
=>|\overrightarrow {AB} + \overrightarrow {BC}|=|\overrightarrow {AC}|=a
Vẽ vectơ đối của \overrightarrow {BC} : là vectơ \overrightarrow {BM}
Ta được : \overrightarrow {BM} =- \overrightarrow {BC}
=> \overrightarrow {AB} - \overrightarrow {BC}=\overrightarrow {AB} + \overrightarrow {BM}=\overrightarrow {AM}
Mặt khác : AB = BC = BM
=> tam giác AMC vuông tại A.
=> AM = a \sqrt{3}
Vậy :   |\overrightarrow {AB} - \overrightarrow {BC}|=|\overrightarrow {AM}|= a\sqrt{3}

==========================================

Văn ôn – Võ luyện :

BÀI 1 : Chứng minh rằng đối mọi tứ giác ABCD bất kỳ, ta luôn có :
  1. \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC}
  2. \overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD}

BÀI 2 : hình vuông ABCD cạnh a. tính độ dài các vectơ :
  1. \overrightarrow {AC} + \overrightarrow {AD}
  2. \overrightarrow {AC} - \overrightarrow {AD}
BÀI 3 :
Người đăng: vào lúc
Nhãn: ,

Không có nhận xét nào:

Đăng nhận xét

Đăng ký: Đăng Nhận xét (Atom)