BÀI 3 HÀM SỐ BẬC hai y = ax2 + bx + c
Khảo sát hàm số bậc nhất y = ax2 + bx + c (a ≠ 0):
TXĐ : D = R.Tọa độ đỉnh I (-b/2a; f(-b/2a)). f(-b/2a) = -Δ/4a
Trục đối xứng : x = -b/2a
Tính biến thiên :
- a > 0 hàm số nghịch biến trên (-∞; -b/2a). và đồng biến trên khoảng (-b/2a; +∞)
- a < 0 hàm số đồng biến trên (-∞; -b/2a). và nghịch biến trên khoảng (-b/2a; +∞)
a > 0
| x | -∞ | -b/2a | +∞ | ||
| y | +∞ |
|
f(-b/2a) |
|
+∞ |
| x | -∞ | -b/2a | +∞ | ||
| y | -∞ |
|
f(-b/2a) |
|
-∞ |
Đồ thị hàm số ax2 + bx + c là một đường parabol (P) có:
- đỉnh I (-b/2a; f(-b/2a)).
- Trục đối xứng : x = -b/2a.
- parabol (P) quay bề lõm lên trên nếu a > 0, parabol (P) quay bề lõm xuống dưới nếu a < 0.
=========================================================
BÀI TẬP SGK :
Bài 2 trang 49 SGKCB :lập bảng biến thiên và vẽ đồ thị hàm số :
a)y = 3x2 – 4x + 1
d)y = -x2 – 4x – 4
giải.
a)y = 3x2 – 4x + 1 ( a = 3; b =-4; c = 1)
TXĐ : D = R.
Tọa độ đỉnh I (2/3; -1/3).
Trục đối xứng : x = 2/3
Tính biến thiên :
a = 3 > 0 hàm số nghịch biến trên (-∞; 2/3). và đồng biến trên khoảng 2/3 ; +∞)
bảng biến thiên :
|
x
|
-∞
|
|
2/3
|
+∞
|
|
|
y
|
+∞
|
|
-1/3
|
|
+∞
|
Các điểm đặc biệt :
(P) giao trục hoành y = 0 : 3x2 – 4x + 1 = 0 <=> x = 1 v x = ½
(P) giao trục tung : x = 0 => y = 1
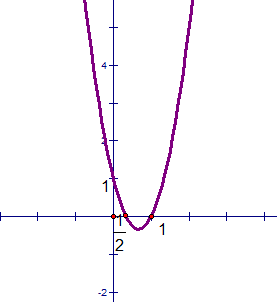
Đồ thị :
Đồ thị hàm số y = 3x2 – 4x + 1 là một đường parabol (P) có:
· đỉnh I(2/3; -1/3).
· Trục đối xứng : x = 2/3.
· parabol (P) quay bề lõm lên trên .
d)y = -x2 + 4x – 4
TXĐ : D = R.
Tọa độ đỉnh I (2; 0).
Trục đối xứng : x = 2
Tính biến thiên :
a = -1 < 0 hàm số đồng biến trên (-∞; 2). và nghịch biến trên khoảng 2 ; +∞)
bảng biến thiên :
|
x
|
-∞
|
|
2
|
+∞
|
|
|
y
|
-∞
|
|
0
|
|
-∞
|
Các điểm đặc biệt :
(P) giao trục hoành y = 0 : -x2 + 4x – 4 = 0 <=> x = 2
(P) giao trục tung : x = 0 => y = -4
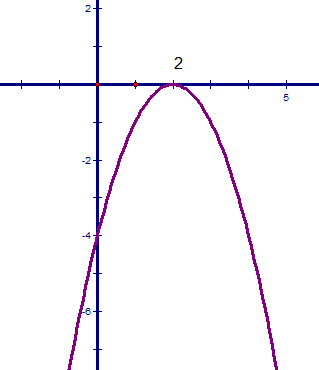
Đồ thị :
Đồ thị hàm số y = -x2 + 4x – 4 là một đường parabol (P) có:
· đỉnh I(2; 0).
· Trục đối xứng : x = 2.
parabol (P) quay bề lõm xuống dưới .===================================================================
BÀI TẬP BỔ SUNG :
BÀI 1 :
Cho hàm số :y = f(x) = ax2 + 2x – 7 (P).
Tìm a để đồ thị (P) đi qua A(1, -2)
GIẢI.
Ta có : A(1, -2)Vậy : y = f(x) = 3x2 + 2x – 7 (P)
BÀI 2 :
Cho hàm số :y = f(x) = ax2 + bx + c (P).
Tìm a, b, c để đồ thị (P) đi qua A(-1, 4) và có đỉnh S(-2, -1).
GIẢI.
Ta có : A(-1, 4)Ta có : S(-2, -1)
(P) có đỉnh S(-2, -1), nên : xS =
Từ (1), (2) và (3), ta có hệ :
Vậy : y = f(x) = 5x2 + 20x + 19 (P)
==========================================
BÀI TẬP RÈN LUYỆN :
BÀI 1 :cho hàm số bậc hai : y = f(x) = x2 + 2mx + 2m – 1 (Pm). đường thẳng (d) : y = 2x – 3
- Khảo sát và vẽ đồ thị của hàm số khi m = 2.
- Tìm m để (Pm) tiếp xúc (d).
- Tìm m để (d) cắt (Pm) tại hai điểm A, B phân biệt sao cho tam giác OAB vuông tại O.
Cho hàm số :y = f(x) = ax2 + bx + 3 (P). tìm phương trình (P) :
- (P) đi qua hai điểm A(1, 0) và B(2, 5).
- (P) tiếp xúc trục hoành tại x = -1.
- (P) đi qua điểm M(-1, 9) và có trục đối xứng là x = -2.
- Khảo sát và vẽ đồ thị của hàm số (P).
- Tìm m để phương trình sau có 4 nghiệm : x2 – 4|x| + 2m – 3 = 0.
- Khảo sát và vẽ đồ thị của hàm số (P).
- Xác định m để (d) cắt (P) tại hai điểm phân biệt A và B thỏa AB = 2.
không hay
Trả lờiXóa