bài 4 một số hệ thức về cạnh và góc trong tam giác vuông

bài 4

một số hệ thức về cạnh và góc trong tam giác vuông

Định lí :

Trong tam giác vuông, mỗi cạnh góc vuông bằng :

a)      Cạnh huyền nhân với sin góc đối hoặc cosin góc kề.

b)      Cạnh góc vuông kia nhân với tang góc đối hoặc cotang góc kề.

Công thức :

AC = BC.sin B = BC.cos C = AB.tg B = AB.cotg C.

AB = BC.sin C = BC.cos B = AC. Tam giác C = AC.cotg B

Áp dụng giải tam giác vuông :

Yêu cầu :

Tìm các cạnh và các góc của tam giác vuông khi cho biết hai yếu tố.

=================================================

BÀI TẬP SGK :

BÀI 27 TRANG 88 :

a)      Cho b = AC = 10cm;
b)      Cho c = AB = 10cm;
c)      Cho a = BC = 20cm;
d)     Cho c = AB = 21cm; b = AC = 18cm
Giải.
a)      Cho b = AC = 10cm;
Nhận xét :

cạnh góc vuông AC kề với góc C.

giải.

xét tam giác ABC vuông tại A, ta có :

(tổng hai góc nhọn trong tam giác vuông)

            = >

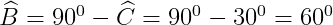
Cạnh góc vuông AB = AC.tgC = 10.tg30⁰ = 10. 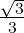cm

Cạnh huyền : AC = BC.cosC

= > BC = AC/cos30⁰ = 20.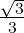 cm

d)      Cho c = AB = 21cm; b = AC = 18cm
Nhận xét :

Biết hai cạnh góc vuông.

Giải.

xét tam giác ABC vuông tại A, theo định lí pitago :

BC² = AB² + AC² = 21² + 18²  = 765

= > BC = 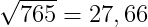cm

tgB =

= >

(tổng hai góc nhọn trong tam giác vuông)

      = >

========================================================

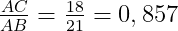
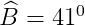
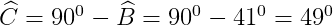
BÀI TẬP RÈN LUYỆN :

BÀI 1 :

 Cho tam giác ABC vuông tại A, có BC = 10cm,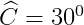

a)      Tính AB, AC.

b)      Đường cao AH.

BÀI 2 :

Cho hình thang cân ABCD đáy lớn AB = 20cm, cạnh bên AD = 8cm,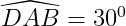

a)      Tính Đường cao DH, đáy nhỏ CHUYểN ĐộNG.

b)      Tính BD,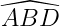

========================================================

ĐỂ KIỂM TRA ĐỊNH HƯỚNG.

ĐỂ KIỂM TRA 1 TIẾT CHƯƠNG I HÌNH HỌC LỚP 9

Thời gian 45 phút.

BÀI 1 :

Cho tam giác ABC có góc A = 90⁰, BC = 10cm, đường cao AH = 4cm, gọi I, K lần lược là chân đường vuông góc kẻ từ H đến AB và AC. Tính :

a)      BH, CH.

b)      AB, AC.

c)      Diện tích tứ giác AIHK.

BÀI 2 :

Giải tam giác ABC vuông tại A trong các trường hợp :

a)      Góc b = 40⁰ và AB = 4cm.

b)      sinC = 0,6 và AC = 6cm.

BÀI 3 :
Cho hình chữ nhật ABCD có đường chéo AC  = 50cm và góc BAC = 30⁰. Tính chu vi và diện tích hình chữ nhật ABCD.

Đề kiểm tra 1 tiết chương 1 hình học lớp 9 (2)

BÀI 1 :
Cho tam giác DEF vuông tại D , đường cao DH. Biết DE = 12cm, DF = 16cm. tính EF, DH, EH.
bài 2 :giải tam giác ABC vuông tại A, có AB  = 10cm, góc B  = 40⁰.
bài 3 :
Cho tam giác ABC vuông tại A, có AB = 6, BC = 10. Có đường cao AH. Gọi E, F là hình chiếu của H lần lược lên AB, AC.

1. Cm : tứ giác AEHF là hình chữ nhật.
2. Tính EF.
3. Cm : AE.AB = AF.AC
4. Tính A = = Sin²B + sin²C – tgB.tgC

Đề tham khảo toán lớp 9 – THCS Trường Toản

Kiểm tra 1 tiết – Hình học chương 1.

Bài 1 : Tính : (không dùng bảng số và máy tính )

sin²35⁰ + tg22⁰ + sin²55⁰ – cotg13⁰ : tg77⁰ – cotg68⁰

Bài 2 : Cho góc nhọn α, sin α = 2/3biết . Không tính số đo góc , hãy tính cosα, tgα , cotgα .
Bài 3 : Cho ΔABC vuông tại A, biết AC = 12cm, BC = 15cm.

a ) Giải tam giác ABC.

b ) Tính độ dài đường cao AH, đường phân giác AD của ΔABC .

Bài 4 : Cho ΔABC có ba góc nhọn, kẻ đường cao AH.

a ) Chứng minh : sinA + cosA > 1.

b ) Chứng minh : BC = AH.(cotgB + cotgC).

c ) Biết AH = 6cm, góc B = 60⁰, góc C = 45⁰. Tính diện tích ΔABC

HẾT.

=======================================================================

Đề kiểm tra giữa học kì I – năm học 2011 – 2012

Môn toán – lớp 9

NGÀY 17 – 10 – 2011

Thời gian 90 phút

Bài 1 (3 điểm) rút gọn biểu thức
a)
b)
c) với 0 < a ≠ 4
Bài 2 (2 điểm) chứng minh đẳng thức :
a)
b)
Bài 3 (1 điểm) tìm x biết :

Bài 4 (1,5 điểm)

giải tam giác ABC vuông tại A trong trường hợp : AB = 4cm; AC = 3cm.

Bài 5 (2,5 điểm)

cho tam giác ABC vuông tại A có đường cao AH, AB = 6cm, AC = 8cm

a) Tính độ dài : BC, HA, HB, HC.

b) Tia phân giác góc BAC cắt BC tại D. tính diện tích tam giác ABD

HẾT.