Bài 4 liên hệ giữa phép chia và phép khai căn
1. Định lí :
Với hai số A không âm, B dương . ta có :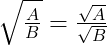
2. Áp dụng :
Quy tắc khai phương một tích :
Muốn khai phương một thương 
của số a không âm, b dương. ta có thể lần lược khai phương từng số a và số b, rồi lấy kết quả thứ nhất chia kết quả thứ hai.
Ví dụ : của số a không âm, b dương. ta có thể lần lược khai phương từng số a và số b, rồi lấy kết quả thứ nhất chia kết quả thứ hai.
Quy tắc nhân các Căn thức bậc hai :
Muốn chia Căn thức bậc hai của số a
không âm cho Căn thức bậc hai của số b dương , ta có thể chia số a cho
số b rồi khai phương các kết quả đó.
Ví dụ : 
3. Bài tập :
Bài 28/T18 : tính
b.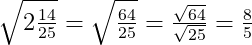 
d.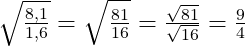 
bài 29/T19 : tính
a.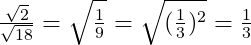 
b.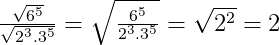
BÀI 30/T19 : rut gọn các biểu thức :
a. A =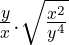 
với x >0 ; y ≠ 0
Ta có :A = với x >0 ; y ≠ 0
(x > 0; y2 > 0)
b. B = 
với y < 0
Ta có : B = với y < 0
(y < 0; x2 ≥ 0)Bài 33 /T 19 : giải phương trình :
a.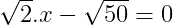 
<=> 
<=> S = {5}
b.
<=> 
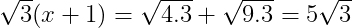
<=> x + 1 = 5
<=> x = 4
Vậy : S = { 4}.
c. 
<=> 
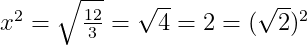
<=> x = ±
Vậy : S = {± }
Không có nhận xét nào:
Đăng nhận xét