BÀI 6 – 7
TAM GIÁC CÂN – TAM GIÁC ĐỀU – TAM GIÁC VUÔNG
1. TAM GIÁC CÂN :
Định nghĩa :
Tam giác cân là tam giác có hai cạnh bằng nhau.
Định lí 1 :
Tam giác cân có hai góc đáy bằng nhau.
Định lí 2 :
Tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
2. TAM GIÁC ĐỀU :
Định nghĩa :
Tam giác đều là tam giác có ba cạnh bằng nhau.
Tính chất :- Trong Tam giác đều có ba góc bằng 600.
- Nếu Tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
- Nếu Tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều.
3. TAM GIÁC VUÔNG :
Định nghĩa :
Tam giác vuông là tam giác có một góc vuông.
Định lí Py-ta-go thuận :
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Định lí Py-ta-go đảo :
Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
=======================
BÀI TẬP SGK :
BÀI TẬP 51 TRANG 128 :A) So sánh :
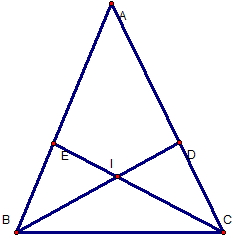 XÉT ΔABD và ΔACE, có :
XÉT ΔABD và ΔACE, có :
AB = AC (ΔABC cân tại A)
AE = AD (gt)
=> ΔABD= ΔACE (c – g -c)=>
b) ΔIBC là tam giác gì ?
ta có :
Hay 
Mà : 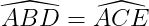 (cmt)
(cmt)
=> => ΔIBC là tam giác cân tại I.
BÀI TẬP 52 TRANG 128 :
XÉT ΔABO và ΔACO, có :

OA cạnh chung.
=> AB = AC (cạnh tương ứng);
=> ΔABC cân tại A (1)
Xét tứ giác ABOC, ta có :
Từ (1) và (2), => ΔABC đều.
BÀI TẬP 54 TRANG 131 :
Ta có : AC = 8,5cm; BC = 7,5cm
 Áp dụng định lí pytago vào ΔABC (
Áp dụng định lí pytago vào ΔABC (AC2 = BA2 + BC2
AB2 = AC2 – BC2
AB2 = 8,52 – 7,52 = 16
=> AB =
==============================
BÀI TẬP RÈN LUYỆN :
Bài 1 :Cho ABC nhọn (AB < AC). Gọi M là trung điểm của BC. Trên tia AM lấy đi ểm N sao cho M là trung điểm của AN.
a/. Ch/m : ΔAMB = ΔNMC
b/. Vẽ CD
c/. Vẽ AH
Ch/m : BI = CN.
Bài 2:
Cho có AB = AC. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AN = AM. Gọi H là trung điểm của BC.
a) Chứng minh: ΔABH = ΔACH
b) Gọi E là giao điểm của AH và MN. Chứng minh: AH
BÀI 3 :
Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD = AB; AE = AC
a) Chứng minh BE = DC
b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 4.Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
BÀI 5.
Cho tam giác ABC có góc A =350 . Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.
a) Chứng minh ΔAHB = ΔDBH.
b) Chứng minh AB//HD.
c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.
d) Tính góc ACB , biết góc BDH= 350 .
Bài 6 :Cho tam giác ABC cân tại A và có
- Tính
và
- Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Chứng minh : DE // BC.
Cho tam giác ABC cân tại A. Lấy D thuộc AC, E thuộc AB sao cho AD = AE.
- Chứng minh : DB = EC.
- Gọi O là giao điểm của BD và EC. Chứng minh : tam giác OBC và ODE là tam giác cân.
- Chứng minh rằng : DE // BC.
Cho tam giác ABC. Tia phân giác của góc C cắt AB tại D. trên tia đối của tia CA lấy điểm E sao cho CE = CB.
- Chứng minh : CD // EB.
- Tia phân giác của góc E cắt CD tại F. vẽ CK vuông góc EF tại K. chứng minh : CK Tia phân giác của góc ECF.
Cho tam giác ABC vuông tại A có
- Tam giác ACE đều.
- A, E, F thẳng hàng.
Cho tam giác ABC (AB <AC). Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc AB tại H. IK vuông góc AC tại K. chứng minh : BH = CK.
=========================================
ĐỀ THI :
Đề kiểm tra học kì I năm học 2008 – 2009 Q1
Môn : toán lớp 7
Thời gian làm bài 90 phút.
BÀI 1 : (2,5 điểm) tính bằng cách hợp lý :
a) 
b) 
c) 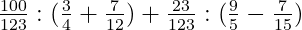
BÀI 2 : (2,5 điểm)Tìm x, biết :
a) 
b) 
c) 33x : 11x = 81
BÀI 3 : (1,5 điểm)Ba đội cày làm việc trên ba cánh đồng có diện tích như nhau. Đội thứ nhất hoàn thành công việc trong 12 ngày. Đội thứ hai hoàn thành công việc trong 9 ngày. Đội thứ ba hoàn thành công việc trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy cày biết Đội thứ hai nhiều hơn Đội thứ nhất 2 máy và năng suất của các máy như nhau.
BÀI 4 : (3,5 điểm)
Cho tam giác ABC vuông góc tại A có góc B = 530.
a) Tính góc C.
b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. cmr : ΔBEA = ΔBED.
c) Qủa C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. cm : ΔBHF = ΔBHC.
d) Cm : ΔBAC = ΔBDF và D, E, F thẳng hàng.
HẾT.
Không có nhận xét nào:
Đăng nhận xét