Bài 1 : Căn bậc hai số học

Bài 1 Căn bậc hai số học

1. Định nghĩa :

Căn bậc hai số học của a là số dương x sao cho x² = a.

Với số dương a,  số được gọi là Căn bậc hai số học của a.

Ta viết :

  x² = a và x ≥ 0

2. Định lí :

Với hai số không âm a và b ta có :

0 ≤ a < b 

===============================================

Bài tập SGK 

bài 1/t6 :tìm Căn bậc hai số học của : 121, 225, 361

Giải .

ta có : 11 ≥ 0 và 11² = 121 vậy  = 11

ta có : 15 ≥ 0 và 15² = 225 vậy 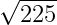 = 15

ta có : 19 ≥ 0 và 19² = 361 vậy  = 19

Nhận xét : 

• ta nhẩm xem một số bình phương bằng 121.
• ta nhẩm được hai số : 11 và -11.
• kết hợp điều kiện ta chọn 11.

bài 2/t6 : so sánh :2 và  ; 7 và
Giải.

Ta có : 2 = ; =

Ta được : 0 ≤ 3 < 4 = >  <  hay < 2

Ta có : 7 = ; =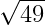

Ta được : 0 ≤ 47 < 49 = >  <  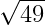hay < 7

PHƯƠNG PHÁP SO SÁNH HAI SỐ CĂN :

Bước 1 : Tìm hai số dưới dấu căn . Ta đưa các số vào bên trong căn.

Bước 2 : so sánh hai số dưới dấu căn. Dùng định lí so sánh, so sánh hai căn.

Bước 3 : Trả về số ban đầu. Kết luận.

———————————————————————————–

bài 4b/7 sgk : tìm số x không âm, biết : 2

giải :

ta được : 

ta có :  7> 0 nên : x =7²  = 49

vậy : x = 49

Bài tập bổ sung :

1. Dạng giải phương trình căn :

bài 1 : 

<=>

<=> x   = 36 (vì 6 > 0)

Vậy : S = {36}

Bài 2 :  

<=>

vì -2 < 0 : phương trình vô nghiệm.

vậy : S = Ø.

2. Dạng giải bất phương trình căn :

Bài 1 : 

<=>

<=>0 ≤ x < 16 (định lí)

Bài 2 :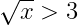 

<=>

<=> 0 ≤ 9 < x (định lí)

<=> x > 9

BÀI TẬP RÈN LUYỆN :

BÀI 1 : so sánh các cặp số

a) 11 và  ; b)  và

BÀI 2 : gỉai  phương trình căn và bất phương trình căn :

a)

b)