BÀI 3 :
Liên hệ giữa DÂY và KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY
Định lí 1 :
Trong một đường tròn :
Hai dây bằng nhau thì cách đều tâm.
Hai dây cách đều tâm thì bằng nhau.
Định lí 2 :
Trong hai dây của một đường tròn :
Dây nào lớn hơn thì dây đó gần tâm hơn .
Dây nào gần tâm hơn thì dây đó lớn hơn .
================================================
BÀI TẬP SGK :
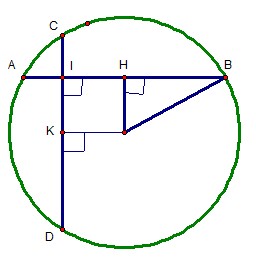
BÀI 12 TRANG 206 :Kẻ OH vuông góc AB tại H, OK vuông góc CD tại K.
a) Tính OH :
OH vuông góc AB tại H = > HA = HA = AB/2 = 8/2 = 4cm.
Xét Δ OHB vuông tại H, theo Định lí Pitago :
= > OH2 = OB2 – HB2 = 52 – 42 = 9
= > OH = 3cm.
b) Chứng minh : CD = AB.
Ta có :
AI = 1cm, AH = 4cm = > I nằm giữa AH
= > AH = AI + IH = > IH = 3cm.
= > IH = OH = 3cm.
Xét tứ giác OHIK ta có :
= > tứ giác OHIK là hình chữ nhật
Mà : IH = OH ( cmt)
= > tứ giác OHIK là hình vuông.
= > OH = OK
= > AB = CD—————————————————————————————————————
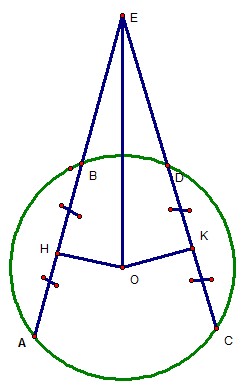
BÀI 13 TRANG 106 :
a) EH = EK
HA = HB = AB/2 (gt) = > OH  AB
AB
KC = KD (gt) = CD/2 = > OK CD
CD
AB = CD = > OH = OK; AH = KC
Xét ΔEOH và tam giác ΔEOK, ta có :
OH = OK(cmt)
= > ΔEOH = ΔEOK
= > EH = EK
b)EA = EC :ta có : EH = EK (cmt)
AH = KC (cmt)
= > EH + AH = EK + KC
< => EA = EC đpcm.
————————————————————————————————————— BÀI 16 TRANG 106 :
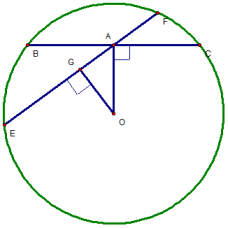
BÀI 16 TRANG 106 :
Kẽ OG  EF tại G.
EF tại G.
Xét 𝛥 OAG vuông tại G, ta có :
OA > OG ( OA là cạnh huyền, OG là cạnh góc vuông)
=> AB < EF.===============================================
BÀI TẬP RÈN LUYỆN :
Bài 1 :Cho đường tròn (O) có AB là đường kính. Vẽ 2 dây AD và BC song song với nhau.
a) AD = BC.
b) CD là đường kính của (O).
Bài 2 :Cho tam giác ABC (AB < AC ), kẻ hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh bốn điểm B, D, C, E cùng thuộc một đường tròn . xác định tâm I của đường tròn đó.
b) Chứng minh AB.AE = AC.AD
c) Gọi K là điểm đối xứng của H qua I. Chứng minh rằng : BHCK là hình bình hành.
d) xác định tâm O của đường tròn qua 4 điểm A, B, K, C.
e) OI // AH.
4, Cho tg ABC có 3 góc nhọn , Vẽ đg cao AD, BE . H là trực tâm
Trả lờiXóaa,Cm tanB*tanC=AD/HD ( câu này mình làm rồi)
b,CM DH*DA=BC^2/4
5,Rút gọn b, B=sqrt(3+sqrt5)-sqrt(3-sqrt5)-sqrt2 c,C=(1+tan^2ALPHA)(1-sin^2ALPHA) +(1+cot^2ALPHA)(1-cos^2ALPHA)
6, Giải pt a, x* sqrtx-2*sqrtx-x=0 b,x^2-5x+36=8*sqrt(3x+4)
7,Cho các số nguyên dương a,b,c đôi 1 nguyên tố cùng nhau tm~ (a+b)c=ab Xét tổng M=a+b có phải là số chính phương không?
8,Cho tg ABC nhọn , Đường cao AD , BE , CF cắt nhau ở H. M là trung điểm HC.N là trung điểm AC AM vuông góc vs HN ở G . Đg thẳng qua M vuông góc vs HC và đthẳng qua N vuông góc vs AC cắt nhau ở K . CMR:a,S(AEF)=S(ABC)*cos^2(^BAC) b, BH*KM=BA*KN c,sqrt((GA^5+GB^5+GH^5)/(GM^5+GK^5+GN^…
9, Cho M cố định thuộc AB . Vẽ về cùng 1 phía của AB tia Ax,By vuông góc vs AB.Qua M có 2đt Mt , Mz thay đổi luôn vuông góc vs nhau ở M , cắt Ax,By theo thứ tự ở C,D . ^AMC=ALPHA . Xác định góc ALPHA để S(MCD)
Giusp em vs m.n ơi , toán 9 khó