BÀI 4 -5

HAI ĐƯỜNG THẲNG SONG SONG

TIÊN ĐỀ Ơ-CLIT

QUAN HỆ TÍNH VUÔNG GÓC VÀ SONG SONG

1.Định nghĩa :

Hai đường thẳng song song là hai đường thẳng không cắt nhau.

Hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song.

2. Dấu hiệu nhận biết hai đường thẳng song song :

Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một căp góc so le trong bằng nhau( hoặc một cặp góc đồng vị bằng nhau ) thì a và b song song nhau.

Ta có c cắt a và b lần lượt tại A và B.

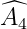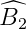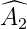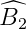Nếu $\widehat{A_4}$ = $\widehat{B_2}$ hoặc $\widehat{A_2}$ = $\widehat{B_2}$ thì a // b.

3. TIÊN ĐỀ Ơ-CLIT :

Qua một điểm ở ngoài đường thẳng chỉ có một và chỉ một đường thẳng song song với đường thẳng đó.

4. Tính chất của hai đường thẳng song song :

Nếu một đường thẳng cắt hai đường thẳng song song thì :

Hai góc đồng vị bằng nhau .
Hai góc so le trong bằng nhau .
Hai góc trong cùng phía bù nhau.

Quan hệ tính vuông góc và song song :

Tính chất 1 :

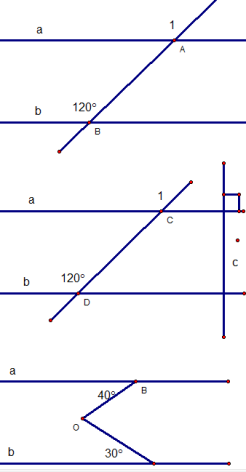
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ 3 thì chúng song song nhau.

Tính chất 2 :

một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc đường thẳng kia.

Tính chất 3 :

Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ 3 thì chúng song song nhau.

================

BÀI TẬP SGK :

BÀI 34 TRANG 94 :
Hình 22 : biết $\widehat{A_4}=37^0$ a // b.

Giải

a)      Tính $\widehat{B_1}$ :
Ta có a // b ,suy ra :
$\widehat{B_1}=\widehat{A_4}=37^0$ ( vì $\widehat{B_1}, \widehat{A_4}$ so le trong)
b)      So sánh $\widehat{A_1}$ và $\widehat{B_4}$ :
$\widehat{A_1} = \widehat{B_4}$ ( vì $\widehat{A_1}$ và $\widehat{B_4}$ đồng vị)
c)      Tính $\widehat{B_2}$ :
Ta có :
$\widehat{B_2}+\widehat{A_4}=180^0$ ( vì $\widehat{B_2}$ và $\widehat{A_4}$ trong cùng phía)
$\widehat{B_2}+\widehat{A_4}=180^0-\widehat{A_4}=180^-47^0=133^0$
BÀI 46 TRANG 98 : Hình 31 : biết
a) vì sao a //b :
ta có :

a $\bot$ AB (gt)

b $\bot$ AB(gt)

=> a // b (cùng vuông góc AB).
b) Tính $\widehat{C_1}$ :

Chứng minh trên : a // b, suy ra :

$\widehat{C_1}+\widehat{D1}=180^0$ (trong cùng phía)

$\widehat{C_1}=180^0-\widehat{D1}=180^0-120^0=60^0$

BÀI 57 TRANG 104 :
Kẻ c // a // b và đi qua O :

Tính x = $\widehat{O_1} +\widehat{O_2}$

Ta có a // c, suy ra :

$\widehat{O_1}=\widehat{A_1}=38^0$ (so le trong)

Ta có b // c, suy ra :

$\widehat{O_2}+\widehat{B_1}=180^0$ (trong cùng phía)

$\widehat{O_2}=180^0-\widehat{B_1}=180^0-132^0=48^0$

x = $\widehat{O_1} +\widehat{O_2}=38^0+48^0=86^0$

==========================

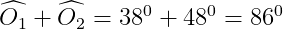
BÀI TẬP BỔ SUNG :

Cho hình :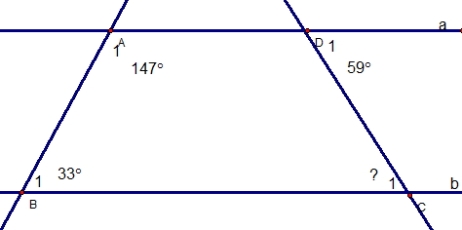

a) Chứng minh : a // b

b) Tính góc C :

Giải.

a) Chứng minh : a // b

Đường thẳng c cắt đường thẳng a, b tại A và B.

Ta có :

$\widehat{A_1} +\widehat{B_1}=147^0+33^0=180^0$

Mà $\widehat{A_1} , \widehat{B_1}$ ở vị trí trong cùng phía, suy ra a // b.

a) Tính góc C :

Theo chứng minh trên : a // b, suy ra :

$\widehat{C_1} =\widehat{D_1}=59^0$ ( soletrong).

=============================

BÀI TẬP RÈN LUYỆN :

BÀI 1 :
Cho $\widehat{xOy} =60^0$ . từ điểm A thuộc tia phân giác của $\widehat{xOy}$ vẽ đường thẳng song song Ox cắt Oy ở B và vẽ đường thẳng song song Oy cắt Ox ở C.

Tính $\widehat{COA}$ và $\widehat{AOB}$ .
Tính $\widehat{BAO}$ và $\widehat{CAO}$ .
CHỨNG MINH : AO là tia phân giác của $\widehat{BAC}$

BÀI 2 :
Cho tam giác ABC có AD là tia phân giác . vẽ tia CE sao cho góc ACE và góc BAC so le trong. Vẽ tia CM tia phân giác của góc ACE. Chứng minh rằng :

AB / / CE
AD // CM

BÀI 3 :
Cho $\widehat{xOy} =30^0$ . từ điểm A trong $\widehat{xOy}$ vẽ đường thẳng cắt Oy ở B sao cho $\widehat{ABy} =30^0$ . Chứng minh rằng : Ox // AB.
========================================

Đề tham khảo toán lớp 7

Đề kiểm tra 1 tiết chương 1 hình học 7

Câu 1 :(1,5 điểm)
Trong hình sau, cho a // b tính $\widehat{A_1}$
Câu 2 :(1,5 điểm)
Cho đoạn thẳng AB dài 3cm. Vẽ đường trung trực của đoạn thẳng AB.
Câu 3 :(3 điểm)
Cho a // b; c $\bot$ a.
Đường thẳng c có vuông góc với đường thẳng b không ? vì sao?
Cho $\widehat{A_1}=115^0$ . tính $\widehat{B_1}$ , $\widehat{A_2}$
Câu 4 :(4 điểm)
Hình vẽ sau đây cho biết : a // b, $\widehat{B=40^0}$ , $\widehat{C=30^0}$ .
Tính $\widehat{BOC}$ .
HẾT.

Toán học phổ thông - SGK

Gia sư toán - lý - hóa tp Hồ Chí Minh

Thứ Bảy, 29 tháng 9, 2012

BÀI 4 -5 : HAI ĐƯỜNG THẲNG SONG SONG TIÊN ĐỀ Ơ-CLIT QUAN HỆ TÍNH VUÔNG GÓC VÀ SONG SONG