Bài 3 : Phương trình đường ELIP

Bài 3

Phương trình đường ELIP

–o0o–

1. Định nghĩa :

đường ELIP là tập hợp các điểm M(x,y) sao cho tổng khoảng cách từ M đến hai điểm F₁ và F₂ là một số không đổi 2a.

(E) : MF₁ + MF₂ = 2a và F₁F₂ = 2c.

2. Phương trình chính tắc đường ELIP:

(E) : $\frac{x^2}{a^2} +\frac{y^2}{b^2} =1$ với : a² – b² = c².

Đoạn thẳng A₁A₂ : trục lớn của (E) với A₁(-a, 0), A₂(a, 0).

Đoạn thẳng B₁B₂ : trục nhỏ của (E) với B₁(0, -b), A₂(0, b).

Hai tiêu điểm : F₁(-c, 0), F₂(c, 0).

===========================================

BÀI TẬP SGK CƠ BẢN :

BÀI 1.a TRANG 88 :
Xác định độ dài các trục, tọa độ các tiêu điểm, tọa độ các đỉnh của elip : (E) : $\frac{x^2}{25^2} +\frac{y^2}{9^2} =1$

Giải.

a² = 25 => a = 5.
b² = 9 => b = 3
c² = a² – b² = 25 – 9 = 16 => c = 4.

tọa độ các đỉnh : A₁(-5, 0), A₂(5, 0), B₁(0, -3), B₂(0, 3).
độ dài các trục lớn : A₁A₂ = 2a = 10.
độ dài các trục nhỏ : B₁B₂ = 2b = 6.
Hai tiêu điểm : F₁(-4, 0), F₂(4, 0).
————————————————————————————————-
BÀI 2 TRANG 88 :
Lập phương trình Elip (E) :

độ dài các trục lớn và độ dài các trục nhỏ là 8 và 6.
độ dài các trục lớn là 10 và tiệu cự bằng 6.

Giải.

độ dài các trục lớn : A₁A₂ = 2a = 8. => a = 4
độ dài các trục nhỏ : B₁B₂ = 2b = 6. => b = 3
Phương trình đường ELIP có dạng (E) : $\frac{x^2}{a^2} +\frac{y^2}{b^2} =1$
Hay : $\frac{x^2}{16} +\frac{y^2}{9} =1$
độ dài các trục lớn : A₁A₂ = 2a = 10 => a = 5
và tiệu cự bằng F₁F₂ = 2c = 6. => c = 3
ta có :c² = a² – b² => b²= a² – c²= 25 – 9 = 16 => b = 4.
Phương trình đường ELIP có dạng (E) : $\frac{x^2}{a^2} +\frac{y^2}{b^2} =1$
Hay : $\frac{x^2}{25} +\frac{y^2}{16} =1$
————————————————————————————————-
BÀI 3 TRANG 88 :
Lập phương trình Elip (E) :

(E) đi qua M(0; 3) và N(3; -12/5).
(E) đi qua M(1 ; $\frac{\sqrt{3}}{2}$ ) và có một tiệu điểm F( $\sqrt{3}$ ; 0).

Giải.
Phương trình đường ELIP có dạng (E) : $\frac{x^2}{a^2} +\frac{y^2}{b^2} =1$
(E) đi qua M(0; 3), nên : $\frac{0}{a^2} +\frac{9}{b^2} =1$
=>b= 3.
(E) đi qua N(3; -12/5), nên : $\frac{9}{a^2} +\frac{144}{25b^2} =1$
=> a = 5.
Phương trình đường ELIP có dạng (E) : $\frac{x^2}{a^2} +\frac{y^2}{b^2} =1$
có tiệu điểm F( $\sqrt{3}$ ; 0) => c = $\sqrt{3}$ => a² – b² = 3 (1)
(E) đi qua M(1 ; $\frac{\sqrt{3}}{2}$ ), nên : $\frac{1}{a^2} +\frac{3}{4b^2} =1$ (2)
Từ (1) và (2) , ta được :
a² = 4 ; b² = 1
vậy : (E) : $\frac{x^2}{4} +\frac{y^2}{1} =1$

=========================================

Văn ôn – Võ luyện :

Câu VII.b.1 đại học khối A 2012 (1,0 điểm)

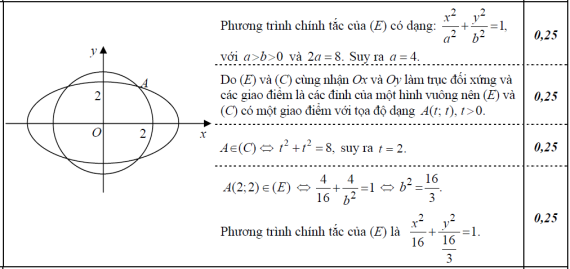
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) : x² + y² = 8. Viết phương trình chính tắc elip (E), biết rằng (E) có độ dài trục lớn bằng 8 và (E) cắt (C) tại bốn điểm tạo thành bốn đỉnh của một hình vuông.

Đáp Án

Câu VI.b.1 đại học khối A 2011 (1,0 điểm)

Trong mặt phẳng tọa độ Oxy, cho elip (E) : $\frac{x^2}{4} +\frac{y^2}{1} =1$ Tìm tọa độ các điểm A và B thuộc (E), có hoành độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.

Đáp Án.

đại học khối D 2002 (1,0 điểm)

Câu VI.b đại học khối B 2012 (1,0 điểm)

1. Trong mặt phẳng toạ độ Oxy, cho điểm A(2; 3) và elip (E): : $\frac{x^2}{3} +\frac{y^2}{2} =1$ . Gọi F₁và F₂là các tiêu điểm của (E) (F₁có hoành độ âm); M là giao điểm có tung độ dương của đường thẳng AF₁với (E); N là điểm đối xứng của F₂qua M. Viết phương trình đường tròn ngoại tiếp tam giác ANF₂.

Câu V đại học khối A 2008
Trong mặt phẳng với hệ tọa độ Oxy, hãy viết phương trình chính tắc của elíp (E) biết rằng (E) có tâm sai bằng $\frac{\sqrt{5}}{3}$ và hình chữ nhật cơ sở của (E) có chu vi bằng 20.
Câu III đại học khối A 2005
Trong mặt phẳng với hệ tọa độ Oxy, cho C(2,0) và phương trình của elíp (E) : $\frac{x^2}{4} +\frac{y^2}{1} =1$ ..tìm hai điểm A và B thuộc (E) sao cho tam giác ABC đều và A và B đối xứng qua trục hoành.

Toán học phổ thông - SGK

Gia sư toán - lý - hóa tp Hồ Chí Minh

Thứ Bảy, 29 tháng 9, 2012