Bài 1 : phương trình đường thẳng

Bài 1

phương trình đường thẳng

–o0o–

1. Khái niệm :

Vectơ $\overrightarrow {u}$ được gọi là vectơ chỉ phương của đường thẳng d nếu $\overrightarrow {u} \neq\overrightarrow {0}$ và giá của $\overrightarrow {u}$ song song hoặc trùng với d.
Vectơ $\overrightarrow {n}$ được gọi là vectơ pháp tuyến của đường thẳng d nếu $\overrightarrow {n} \neq\overrightarrow {0}$ và giá của $\overrightarrow {n}$ vuông góc với vectơ chỉ phương.

2. Phương trình tham số (t ) đường thẳng d :
Đường thẳng d đi qua M(x₀, y₀) và nhận Vectơ $\overrightarrow {u}=(u_1,u_2)$ làm vectơ chỉ phương.

$(d):\begin{cases} x=x_0+u_1.t \\ y=y_0+u_2.t\end{cases}$

Hệ số góc của đường thẳng d : $k=\frac{u_2}{u_1}$
3. Phương trình tổng quát đường thẳng d : ax + by + c = 0
Đường thẳng d đi qua M(x₀, y₀) và nhận Vectơ $\overrightarrow {n}=(a, b)$ làm vectơ pháp tuyến.

a(x – x₀) + b(y – y₀) = 0

4. Vị trí tương đối của hai đường thẳng:
Cho d₁ : a₁x + b₁y + c₁ = 0 và d₂ : a₂x + b₂y + c₂ = 0
Tọa độ giao điểm của d₁ và d₂ là nghiệm của hệ :
$(d):\begin{cases} a_1x + b_1y + c_1 = 0 \\ a_2x + b_2y + c_2 = 0\end{cases}(*)$

Hệ (*) có một nghiệm (x₀, y₀) thì d₁ cắt d₂ tại A(x₀, y₀).
Hệ (*) có vô số nghiệm thì d₁ trùng d₂
Hệ (*) vô nghiệm thì d₁ song song d₂

5. Góc α giữa hai đường thẳng :
d₁ : a₁x + b₁y + c₁ = 0 và d₂ : a₂x + b₂y + c₂ = 0

$cos\alpha=\frac{ |a_1a_2+b_1b_2| }{\sqrt{a_1^2+b_1^2} . \sqrt{a_2^2+b_2^2}}$

6. Khoảng cách từ M(x₀, y₀) đến đường thẳng Δ : ax + by + c = 0

$d(M, \Delta)=\frac{ | ax_0 + by_0 + c | }{\sqrt{a^2+b^2}}$

===========================================

BÀI TẬP SGK :

BÀI 1 TRANG 80 SGK CB :
Lập Phương trình tham số đường thẳng d trong các trường hợp sau :

a) d đi qua M(2;1) và nhận Vectơ 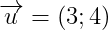$\overrightarrow {u}=(3;4)$ làm vectơ chỉ phương.

b) d đi qua M(-2;3) và nhận Vectơ 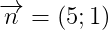$\overrightarrow {n}=(5;1)$ làm vectơ pháp tuyến.

giải.

a) Phương trình tham số đường thẳng có dạng $(d):\begin{cases} x=x_0+u_1.t \\ y=y_0+u_2.t\end{cases}$
$\Leftrightarrow\begin{cases} x=2+3t \\ y=1+4t\end{cases}(d)$
b) Vectơ $\overrightarrow {n}=(5;1)$ làm vectơ pháp tuyến => vectơ chỉ phương $\overrightarrow {u}=(1;-5)$ .
Phương trình tham số đường thẳng có dạng $(d):\begin{cases} x=x_0+u_1.t \\ y=y_0+u_2.t\end{cases}$
$\Leftrightarrow\begin{cases} x=-2+t \\ y=3-5t\end{cases}(d)$
Nhận xét : Lập Phương trình tham số đường thẳng :

Bước 1 : phải tìm điểm đi qua M(x₀, y₀) và nhận Vectơ $\overrightarrow {u}=(u_1,u_2)$ làm vectơ chỉ phương.
Bước 2 : thế số vào công thức.

——————————————————————————————————–
BÀI 2 TRANG 80 SGK CB :

Lập Phương trình tổng quát đường thẳng d trong các trường hợp sau :

a)d đi qua M(-5;-8) có hệ số góc k = -3.

b)d đi qua A(2;1) và B(-4;5)

Giải.

a)d có hệ số góc k = -3 => d : y = -3x + b

d đi qua A(2;1) nên : 1 = -3.2 + b => b = 7

vậy d : y = -3x + 7 hay 3x + y – 7 = 0

b) d nhận vectơ chỉ phương $\overrightarrow {AB}=(-4-2;5-1)=(-6;4)$ => vectơ pháp tuyến $\overrightarrow {n}=(4;6)$ .
=> d : 4(x – 2) + 6(y – 1) = 0
<=> 4x + 6y – 14 = 0
vậy : 2x + 3y – 7 = 0 (d)
Nhận xét : Lập Phương trình tổng quát đường thẳng :

Bước 1 : phải tìm điểm đi qua M(x₀, y₀) và nhận Vectơ $\overrightarrow {n}=(a;b)$ làm vectơ pháp tuyến.
Bước 2 : thế số vào công thức.

—————————————————————————————————————
BÀI 3 TRANG 80 SGK CB :

Cho tam giác ABC. Biết A(1;4), B(3;-1) và C(6;2).

Lập Phương trình tổng quát đường thẳng AB, BC và CA.

Lập Phương trình tổng quát đường cao AH và trung tuyến AM.

Giải.

(AB) nhận vectơ chỉ phương $\overrightarrow {AB}=(3-1;-1-4)=(2;-5)$
=> vectơ pháp tuyến $\overrightarrow {n}=(5;2)$ .
=> (AB) : 5(x – 1) + 2(y – 4) = 0
<=> 5x + 2y – 13 = 0
(AC) nhận vectơ chỉ phương $\overrightarrow {AC}=(6-1;2-4)=(5;-2)$
=> vectơ pháp tuyến $\overrightarrow {n}=(2;5)$ .
=> (AC) : 2(x – 1) + 5(y – 4) = 0
<=> 5x + 2y – 22 = 0
(BC) nhận vectơ chỉ phương $\overrightarrow {BC}=(3-6;-1-2)=(-3;-3)$
=> vectơ pháp tuyến $\overrightarrow {n}=(3;-3)$ .
=> (AB) : 3(x – 6) - 3(y – 2) = 0
<=> x – y – 4 = 0
AH $\bot$ BC => (AH) vectơ pháp tuyến $\overrightarrow {n}=(-3;-3)$ .
(AH) : -3(x – 1) – 3(y – 4) = 0
<=> x + y – 5 = 0
M (x; y) trung điểm BC : $\begin{cases} x=\frac{x_B+x_C}{2}=\frac{9}{2}\\ y=\frac{y_B+y_C}{2}=\frac{1}{2}\end{cases}(d)$
(AM) nhận vectơ chỉ phương $\overrightarrow{AM}=(\frac{7}{2};-\frac{7}{2})$
=> vectơ pháp tuyến $\overrightarrow{n}=(\frac{7}{2};\frac{7}{2})$ .
=> (AM) : (x – 1)7/2 + (y – 4)7/2 = 0
<=> x – y – 5 = 0
Nhận xét :

$\overrightarrow{u}=(a,b)$ và $\overrightarrow{u}\bot\overrightarrow{v}$

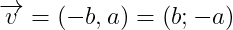=> $\overrightarrow{v}=(-b,a) = (b;-a)$ vì $\overrightarrow{u}.\overrightarrow{v}=ab-ab=0$

——————————————————————————-
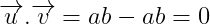
BÀI 6 TRANG 80 SGK CB :
Phương trình tham số đường thẳng $(d): \begin{cases} x=2+2t \\ y=3+t\end{cases}$
Tìm M thuộc d và cách A(0;1) một khoảng 5.

Giải.

M(x;y) thuộc d, nên : M(2 + 2t ; 3 + t).
AM = 5

⇔ AM² = 25

⇔ (2 + 2t – 0)² + (3 + t – 1)² = 25

⇔ 5t²+ 12t – 17 = 0

⇔ t = 1 hoặc t = -17/5

vậy : M(4 ; 4) hoặc M(-24/5 ; -2/5).
——————————————————————————-
BÀI 7 TRANG 81 SGK CB :
Góc góc α giữa hai đường thẳng :
d₁ : 4x – 2y + 6 = 0 và d₂ : x – 3y + 1 = 0

giải.

$cos\alpha=\frac{ |4.1+(-2)(-3)| }{\sqrt{4^2+2^2} . \sqrt{1^2+3^2}}=\frac{\sqrt{2}}{2}$
=> α = 45⁰.
——————————————————————————-
BÀI 9 TRANG 81 SGK CB :
Tìm bán kính đường tròn tâm C(-2 ; -2) tiếp xúc d : 5x+ 12y – 10 = 0

Giải.

đường tròn tâm C(-2 ; -2) tiếp xúc d : $R=d(M, \Delta)=\frac{ |5(-2)+12(-2)-10| }{\sqrt{5^2+12^2}}=\frac{44}{13}$

=============================================

Đại học khối A 2012 (1,0 điểm)

Câu VI.a Đại học khối A 2010 (1,0 điểm)

1. Trong mặt phẳng toạ độ Oxy, cho tam giác ABC cân tại A có đỉnh A(6; 6); đường thẳng đi qua trung điểm của các cạnh AB và AC có phương trình x + y − 4 = 0. Tìm toạ độ các đỉnh B và C, biết điểm E(1; −3) nằm trên đường cao đi qua đỉnh C của tam giác đã cho.

Đáp Án :

=========================================

Văn ôn – Võ luyện :

Câu 7.a (1,0 điểm) Đại học khối A 2012:

Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm của cạnh BC, N là điểm trên cạnh CD sao cho CN = 2ND. Giả sử M(11/2; 1/2) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.

Câu VI.a.1 Cao Đẳng 2011 (1,0 điểm)

Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: x +y = 3. Viết phương trình đường thẳng đi qua điểm A(2; − 4) và tạo với đường thẳng d một góc bằng 45⁰.

Câu VI.a Đại học khối D 2011 (1,0 điểm)

1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh B(– 4; 1), trọng tâm G(1; 1) và đường thẳng chứa phân giác trong của góc A có phương trình x – y – 1 = 0. Tìm tọa độ các đỉnh A và C.

Câu VI.a.1 Đại học khối B 2011 (1,0 điểm)

1. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng Δ: x – y – 4 = 0 và d: 2x – y – 2 = 0. Tìm tọa độ điểm N thuộc đường thẳng d sao cho đường thẳng ON cắt đường thẳng Δ tại điểm M thỏa mãn OM.ON = 8.

Câu VI.a.1 Đại học khối B 2010 (1,0 điểm)

1. Trong mặt phẳng toạ độ Oxy, cho tam giác ABC vuông tại A, có đỉnh C(− 4; 1), phân giác trong góc A có phương trình x + y − 5 = 0. Viết phương trình đường thẳng BC, biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương.

Câu VI.a.1 Đại học khối D 2010 (1,0 điểm)

Câu VI.a (1,0 điểm)
1. Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có đỉnh A(3; −7), trực tâm là H(3; −1), tâm đường tròn ngoại tiếp là I(−2; 0). Xác định tọa độ đỉnh C, biết C có hoành độ dương.

Câu VI.b (1,0 điểm)
1. Trong mặt phẳng tọa độ Oxy, cho điểm A(0; 2) và Δ là đường thẳng đi qua O. Gọi H là hình chiếu vuông góc của A trên Δ. Viết phương trình đường thẳng Δ, biết khoảng cách từ H đến trục hoành bằng AH.

Câu VI.a.1 Đại học khối A 2009 (1,0 điểm)
1. Trong mặt phẳng với hệ toạ độ Oxy cho hình chữ nhật ABCD có điểm I (6;2)là giao điểm của hai đường chéoAC và BD. Điểm M(1;5) thuộc đường thẳng AB và trung điểm E của cạnh thuộc đường thẳng CD:x + y – 5 = 0. Viết phương trình đường thẳngAB.

Toán học phổ thông - SGK

Gia sư toán - lý - hóa tp Hồ Chí Minh

Thứ Bảy, 29 tháng 9, 2012